最近大热的流浪气球，关于用了多少氦气争论不断，下面我们来算算氦气的用量到底需要多少。

一、已知条件

已知：气球直径约60米，漂行高度约18000米。

推算：根据 1976美国标准大气模型，18000高度的大气压约为7505帕斯卡(Pa)，温度约为-56.5摄氏度（216.65K）。

二、计算过程

2.1 18000米高度的空气密度

根据理想气体状态方程，可以计算得到空气的密度为：

$$\rho = \frac{p} {R \times T}$$

其中，ρ表示空气的密度，p表示大气压力，R表示空气的气体常数，T表示温度。 在The Engineering ToolBox 查得空气的R值为 287.05 J/(kg*K)。

将温度和大气压力代入上式，可得：

$$\rho = \frac{7505} {287.058 \times 216.65} = 0.1207(kg/m^3) $$

因此，在18000米高空，空气的密度约为 0.1207 kg/m³。

可以直接在 The Engineering ToolBox 查表：

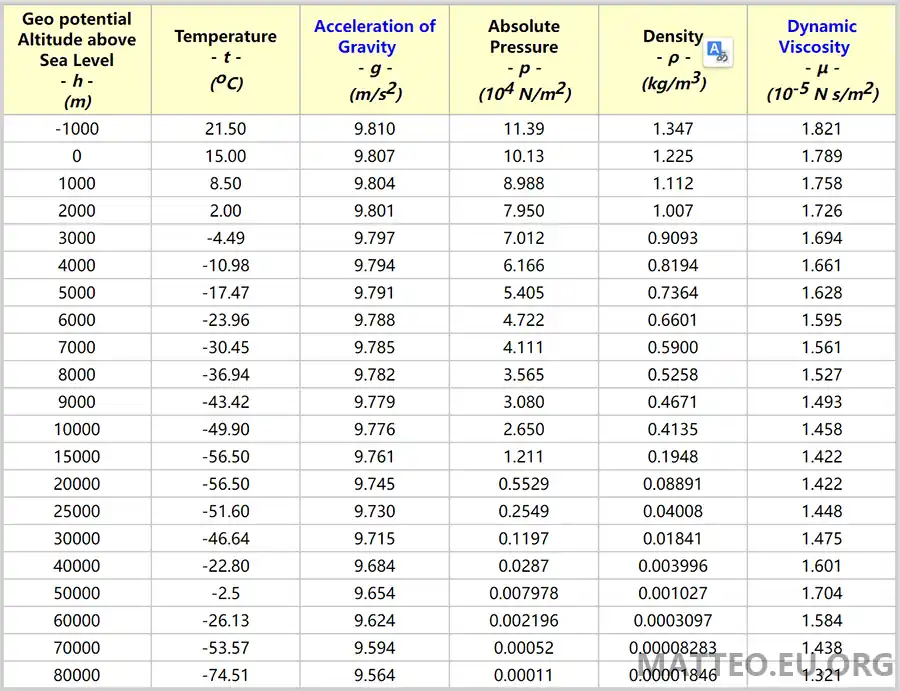
2.2 18000高度的氦气密度

在18000米高空大气压和温度一样，在The Engineering ToolBox 查得氦气的R值为 2077.1 J/(kg*K)。

根据理想气体状态方程，可以计算得到氦气的密度： $$\rho = \frac{7505} {2077.1 \times 216.65} = 0.01668(kg/m^3) $$

因此，在18000米高度上，氦气的密度约为 0.01668 kg/m³。

2.3 直径60米的气球在18000米高度可以提供多少升力？

根据阿基米德原理，气球在空气中受到的浮力大小等于它排开的空气重量。

气球直径为60米，可以计算出气球的体积为：

$$V = \frac{4}{3}\times \pi \times r^3 = \frac{4}{3} \times π \times 30^3 \approx 113097 (m^3)$$

因此，气球排开的气体质量为：

m = ρV = 0.1207 kg/m³ × 113097 m³ ≈ 13650 kg

氦气的质量为：

n= 0.01668 kg/m³ × 113097 m³ ≈ 1886 kg

所以，气球在18000米高空可以提供的浮力为 13650 - 1886 = 11764 kg.

流浪气球能在18000米高度悬浮，说明气球在充满纯氦状态下（这基本不可能），外皮和外挂的重量约为11.8吨。

2.4 需要多少氦气

由上可知需要氦气 1886 kg，液氦的密度为125 kg/m³，1886/125 = 15 m³ 的液氦。

在标准大气压25摄氏度的情况下，1m³ 液氦 = 760m³ 氦气。

所以，如果在18000米高空用纯氦充满直径为60米的气球，需要 15 m³ 液氦 = 11467 m³ 氦气

三、结论

直径60米的流浪气球漂行在18000米的高空，如果是理想状态，气球内压和外压相同（一般会多充一点使内压大于外压，以防气球变形），里面的气体有以下几种情况：

1. 如果充满纯氦，那么需要 15 m³ 液氦，气球外皮+外挂重量 = 11.8 吨。

2. 如果除了氦气，还加了氢气，气球外皮+外挂重量 > 11.8 吨

3. 如果除了氦气，还加了氢气以外的气，气球外皮+外挂重量 < 11.8 吨

4. 一点氦气也没有，只加了别的气，气球外皮+外挂重量 = ？

猜测是第3或第4种情况，因为怎么看也用不着11.8吨，应该加了很多便宜又稳定的气，如氮气。

或者，一点氦气也没有。